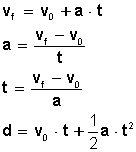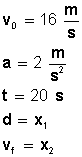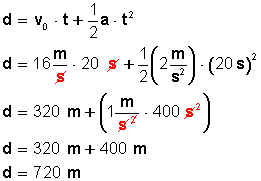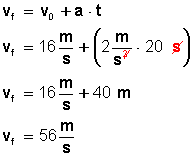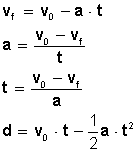Fisiquistas

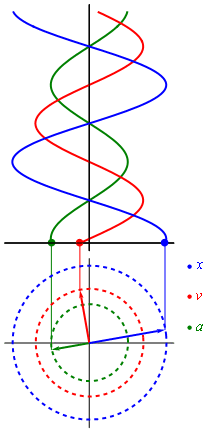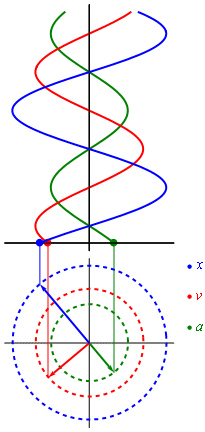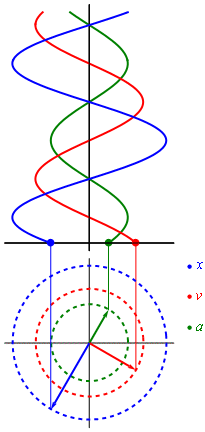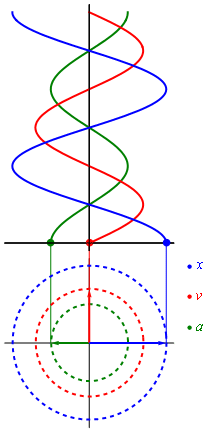
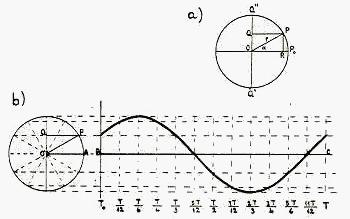
Uniformemente desacelerado es el movimiento cuya aceleración es opuesta al sentido de avance.
Significa aceleración constante opuesta al movimiento que origina que la velocidad disminuya.
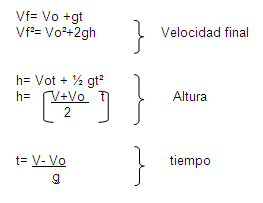
s=vot+1/2at^2
v^2=vo^2+2as
v=vo+at
s=desplazamiento (x, y, cualquier otro en algún sentido)
vo=velocidad inicial
v=velocidad final
t=tiempo
a=aceleración constante
(si la aceleración es desaceleración=desceleración, su signo en las ecuaciones es menos).

Están, pues, dotados de una aceleración que aunque negativa es constante. De ahí que todas las fórmulas cinemáticas deducidas para los movimientos uniformemente acelerados sirvan para describir los movimientos uniformemente retardados sin más que considerar a con su signo, que es, en este caso, negativo.

Se podría decir que un movimiento uniformemente desacelerado es lo mismo que acelerado, pero en este cambia su signo, y en este caso es negativo, aquí se deja un pequeño video explicando el movimiento uniformemente acelerado, solo habría que cambiar el signo a negativo ya que la pendiente es negativa osea, hacia abajo.

En física, el movimiento circular uniforme describe el movimiento de un cuerpo atravesando, con rapidez constante, una trayectoria circular.
Aunque la rapidez del objeto es constante, su velocidad no lo es: La velocidad, una magnitud vectorial, tangente a la trayectoria, en cada instante cambia de dirección. Esta circunstancia implica la existencia de una aceleración que, si bien en este caso no varía al módulo de la velocidad, sí varía su dirección.



Simulador de movimiento circular uniforme:

http://www.ing.uc.edu.ve/~vbarrios/fisica1/fisica1_tutoriales/MovimientoCircular.htm



Es un movimiento en dos dimensiones:







w representa la derivada de q respecto del tiempo y se le conoce como rapidez angular. A mayor rapidez angular, mayor magnitud de la velocidad. Igualmente con el radio R.
La aceleración se calcula derivando la velocidad respecto del tiempo:

Definición: es un movimiento vibratorio bajo la acción de una fuerza recuperadora elástica, proporcional al desplazamiento y en ausencia de todo rozamiento.
Solemos decir que el sonido de una determinada nota musical se representa gráficamente por la función seno. Ésta representa un movimiento vibratorio llamado movimiento armónico simple, que es aquel que se obtiene cuando los desplazamientos del cuerpo vibrante son directamente proporcionales a las fuerzas causantes de este desplazamiento.
Un ejemplo de este movimiento se puede encontrar a partir del desplazamiento de un punto cualquiera alrededor de toda la longitud de una circunferencia.
Cuando un punto (P) recorre una circunferencia con velocidad uniforme, su proyección (Q) sobre cualquiera de los diámetros de esta, realiza un tipo de movimiento armónico simple. Cada vez que el punto se encuentre en uno de los cuatro cuadrantes de la circunferencia, se trazará una perpendicular desde el punto a un diámetro fijo de la circunferencia. A medida que el punto escogido se mueve a velocidad uniforme, el punto proyectado en el diámetro, realizará un movimiento oscilatorio rectilíneo.
Para representar gráficamente (en una función) el movimiento armónico simple de un punto, se toman como abscisas los tiempos medidos como fracciones del período (T/12, T/6, T/4...) que es el tiempo que este punto tarda en dar una vuelta completa a la circunferencia; y como a ordenadas las sucesivas prolongaciones del mismo. La resultante es una sinusoide, ya que la variación del tiempo t, se traduce como una variación del sin x, donde x es el ángulo que forma el radio con el semi-eje positivo de abscisas (x es proporcional al tiempo).

Elementos:
1. Oscilación o vibración: es el movimiento realizado desde cualquier posición hasta regresar de nuevo a ella pasando por las posiciones intermedias.
2. Elongación: es el desplazamiento de la partícula que oscila desde la posición de equilibrio hasta cualquier posición en un instante dado.
3. Amplitud: es la máxima elongación, es decir, el desplazamiento máximo a partir de la posición de equilibrio.
4. Periodo: es el tiempo requerido para realizar una oscilación o vibración completa. Se designa con la letra "t".
5. Frecuencia: es el número de oscilación o vibración realizadas en la unidad de tiempo.
6. Posición de equilibrio: es la posición en la cual no actúa ninguna fuerza neta sobre la partícula oscilante.
Relación entre el M.A.S. y el Movimiento Circular Uniforme
El M.A.S. de un cuerpo real se puede considerar como el movimiento de la "proyección" (sombra que proyecta) de un cuerpo auxiliar que describiese un movimiento circular uniforme (­M.C.U.) de radio igual a la amplitud A y velocidad angular ω, sobre el diαmetro vertical de la circunferencia que recorre.
En lo siguiente podrás visualizar dicha relación.
Vamos a establecer una relación entre un movimiento vobratorio armónico simple y el movimiento circular uniforme. Esto nos va a permitir dos cosas:
- Hallar la ecuación del MAS sin tener que recurrir a cálculos matemáticos complejos.
- Conocer de donde vienen algunos de los conceptos que usamos en el MAS, como frecuencia angular o el desfase.
Observando el applet que viene a continuación. Tememos inicialmente el resorte azul, que oscila verticalmente. En la circunferencia tienes un punto negro que gira con movimiento circular uniforme, ocupando en cada instante una posición en la circunferencia. Traza mentalmente la proyección de esa posición sobre el diámetro vertical de la circunferencia. En cada momento, la masa que cuelga del resorte ocupa una posición determinada.  Observa que la posición de la masa del resorte coincide exactamente con la proyección de la posición del objeto sobre el diámetro, que verás en forma de línea azul en el diámetro vertical.
Es decir, como resumen, cuando un objeto gira con movimiento circular uniforme en una trayectoria circular, el movimiento de la proyección del objeto sobre el diámetro es un movimiento armónico simple.

Lo mismo podríamos decir del resorte amarillo y la proyección sobre el diámetro horizontal, que verás como un trazo amarillo sobre dicho diámetro.
Los vectores azul y amarillo, que varían en el applet, corresponden al valor de la velocidad del resorte, azul para diámetro vertical y amarillo para el horizontal. Observa su variación y comprobarás que la velocidad es máxima en el centro de equilibrio del resorte y mínima en los extremos, en los puntos de mínima y máxima elongación. Observa también como el vector rojo de la gráfica de la derecha, la velocidad del MAS, coincide con el vector azul, la velocidad de la proyección sobre el diámetro vertical, lo que supone una prueba más de lo que hemos afirmado anteriormente.
Ecuaciones del Movimiento Armónico Simple
Fórmulas:
x = A . cos . w . t
x = elongación
r = A = radio
t = tiempo
w = velocidad angular
Vx = - V . sen Ø
V = w . r
h = w . t
w . t = V = Vector representativo de la velocidad lineal.
Vx = proyección de "Y" sobre el eje "X"
h = ángulo
Vx = -2 . F . A . sen (2 . )
Vx = + w " A2 - x2
Ax = - w2 . A . cos. w . t
Ax = - Ac . cos Ø
Ac = proyección de aceleración sobre el eje horizontal
Ac = w2 . x
Ac = aceleración centrípeta
t = 2 " mk
T = periodo

Caída Libre
Se conoce como caída libre cuando desde cierta altura un cuerpo se deja caer para permitir que la fuerza de gravedad actué sobre el, siendo su velocidad inicial cero.
En este movimientos el desplazamiento es en una sola dirección que corresponde al eje vertical (eje "Y").
Es un movimiento uniformemente acelerado y la aceleración que actúa sobre los cuerpos es la de gravedad representada por la letra g, como la aceleración de la gravedad aumenta la velocidad del cuerpo, la aceleración se toma positiva.
En el vacío, todos los cuerpos tienden a caer con igual velocidad.
Un objeto al caer libremente está bajo la influencia única de la gravedad. Se conoce como aceleración de la gravedad. Y se define como la variación de velocidad que experimentan los cuerpos en su caída libre. El valor de la aceleración que experimenta cualquier masa sometida a una fuerza constante depende de la intensidad de esa fuerza y ésta, en el caso de la caída de los cuerpos, no es más que la atracción de la Tierra.
Todos los cuerpos con este tipo de movimiento tienen una aceleración dirigida hacia abajo cuyo valor depende del lugar en el que se encuentren. los cuerpos dejados en caída libre aumentan su velocidad (hacia abajo) en 9,8 m/s cada segundo .
La aceleración de gravedad es la misma para todos los objetos y es independiente de las masas de éstos.
En la caída libre no se tiene en cuenta la resistencia del aire. Si se desprecia la resistencia del aire y se supone que aceleración en caída libre no varía con la altitud, entonces el movimiento vertical de un objeto que cae libremente es equivalente al movimiento con aceleración constante.

                      Leyes fundamentales de la Caída Libre

a) Todo cuerpo que cae libremente tiene una trayectoria vertical
b) La caída de los cuerpos es un movimiento uniformemente acelerado
c) Todos los cuerpos caen con la misma aceleración.
 Los valores de la gravedad son:

Velocidad inicial: normalmente es la velocidad que se le imprime inicialmente a un objeto para ponerlo en movimiento. En este caso como no se le da una fuerza sino solo se deja caer la Vo es igual a cero.
Velocidad final: es la velocidad que alcanzara el objeto cuando llega al punto final de la caída.
Tiempo: Es lo que se demora el cuerpo en caer.
Altura: la altura es la medida de longitud de una trayectoria o desplazamiento, siempre y cuando la medida se tomada como punto de refencia la vertical.

El movimiento rectilíneo uniformemente acelerado (MRUA), también conocido como movimiento rectilíneo uniformemente variado (MRUV), es aquel en el que un móvil se desplaza sobre una trayectoria recta estando sometido a una aceleración constante.
Un ejemplo de este tipo de movimiento es el de caída libre vertical, en el cual la aceleración interviniente, y considerada constante, es la que corresponde a la gravedad.
También puede definirse el movimiento como el que realiza una partícula que partiendo del reposo es acelerada por una fuerza constante.
El movimiento rectilíneo uniformemente acelerado (MRUA) es un caso particular del movimiento uniformemente acelerado (MUA).
                         

Ya vimos que el movimiento rectilíneo puede expresarse o presentarse como
Movimiento rectilíneo uniforme,
o como
Movimiento rectilíneo uniformemente acelerado.
Este último puede, a su vez, presentarse como de caída libre o de subida o tiro vertical.
El movimiento rectilíneo uniformemente aceleradoes un tipo de movimiento frecuente en la naturaleza. Una bola que rueda por un plano inclinado o una piedra que cae en el vacío desde lo alto de un edificio son cuerpos que se mueven ganando velocidad con el tiempo de un modo aproximadamente uniforme; es decir, con una aceleración constante.
Este es el significado del movimiento uniformemente acelerado, el cual “en tiempos iguales, adquiere iguales incrementos de rapidez”.
En este tipo de movimiento sobre la partícula u objeto actúa una fuerza que puede ser externa o interna.
En este movimiento la velocidad es variable, nunca permanece constante; lo que si es constante es la aceleración.
Entenderemos como aceleración la variación de la velocidad con respecto al tiempo. Pudiendo ser este cambio en la magnitud (rapidez), en la dirección o en ambos.
Las variables que entran en juego (con sus respectivas unidades de medida) al estudiar este tipo de movimiento son:
Velocidad inicial           Vo (m/s)
Velocidad final              Vf  (m/s)
Aceleración                     a  (m/s²)
Tiempo                             t   (s)
Distancia                         d  (m)

Para efectuar  cálculos que permitan resolver problemas usaremos las siguientes fórmulas:

Consejos o datos para resolver problemas:
La primera condición será obtener los valores numéricos de tres de las cinco variables. Definir la ecuación que refleje esas tres variables. Despejar y resolver numéricamente la variable desconocida.
Tener cuidado con que en algunas ocasiones un dato puede venir disfrazado; por ejemplo:
"un móvil que parte del reposo.....", significa que su velocidad inicial es Vo = 0 ; "en una prueba de frenado...", significa que su velocidad final es Vf = 0.
Veamos un problema como ejemplo
En dirección hacia el sur, un tren viaja inicialmente a 16m/s; si recibe una aceleración constante de 2 m/s². ¿Qué tan lejos llegará al cabo de 20 s.? ¿Cuál será su velocidad final en el mismo tiempo?
Veamos los datos que tenemos:

Conocemos tres de las cinco variables, entonces, apliquemos  las  fórmulas:
Averigüemos primero la distancia que recorrerá durante los 20 segundos:

Conozcamos ahora la velocidad final del tren, transcurridos los 20 segundos:

Respuestas:
Si nuestro tren, que viaja a 16 m/s, es acelerado a 2 m/s recorrerá 720 metros durante 20 segundos y alcanzará una velocidad de 56 m/s.

Movimiento rectilíneo uniformemente retardado
En los movimientos uniformemente decelerados o retardados la velocidad disminuye con el tiempo a ritmo constante. Están, pues, dotados de una aceleración que aunque negativa es constante. De ahí que todas las fórmulas usadas para los movimientos uniformemente acelerados sirvan para describir los movimientos uniformemente retardados, considerando sólo que su signo es negativo.
Por lo tanto, para efectuar cálculos que permitan resolver problemas que involucren aceleración negativa o deceleración, usaremos las siguientes fórmulas:

Movimiento Rectilíneo Uniformemente Variado (MRUV)

Un movimiento es rectilíneo cuando el cuerpo describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Nos referimos a él mediante el acrónimo MRU.
El MRU (movimiento rectilíneo uniforme) se caracteriza por:

• Movimiento que se realiza sobre una línea recta.
• Velocidad constante; implica magnitud y dirección constantes.
• La magnitud de la velocidad recibe el nombre de aceleridad o rapidez.
• Aceleración nula.

Características

La distancia recorrida se calcula multiplicando la magnitud de la velocidad media velocidad o rapidez por el tiempo transcurrido. Esta relación también es aplicable si la trayectoria no es rectilínea, con tal que la rapidez o módulo de la velocidad sea constante llamado movimiento de un cuerpo.
Al representar gráficamente la velocidad en función del tiempo se obtiene una recta paralela al eje de abscisas (tiempo). Además, el área bajo la recta producida representa la distancia recorrida.
La representación gráfica de la distancia recorrida en función del tiempo da lugar a una recta cuya pendiente se corresponde con la velocidad.
Por lo tanto el movimiento puede considerarse en dos sentidos; una velocidad negativa representa un movimiento en dirección contraria al sentido que convencionalmente hayamos adoptado como positivo.


A continuación se muestra un video explicativo de este movimiento